

previous: Lösung zu Aufgabe 89
next: Lösung zu Aufgabe 91
(a) 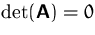 , (b)
, (b) 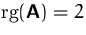 , (c) linear abhängig, da
, (c) linear abhängig, da 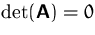 bzw. da
bzw. da 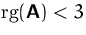 , (d) nicht invertierbar, da
, (d) nicht invertierbar, da 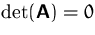 ,
,
(e) 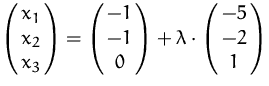 ,
, 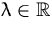 , (f)
, (f) 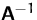 existiert nicht (wegen (d)).
existiert nicht (wegen (d)).


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
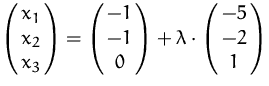 ,
, ![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)