

previous: 19. Februar 1996
next: 14. November 1995
Bestimmen Sie die Hessematrix der Funktion
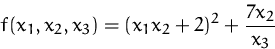
(Lösung)
Gegeben ist die Matrix
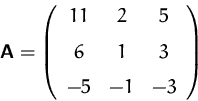
- (a)
- Bestimmen Sie die Inverse zu
 .
. - (b)
- Geben Sie an, wie genau ein Element der Matrix verändert
werden kann, so daß
 nicht mehr invertierbar ist.
nicht mehr invertierbar ist.
(Lösung)
Gegeben ist die Matrixgleichung
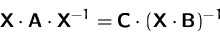
- (a)
- Geben Sie an, welche Beschränkungen es für die Zeilenanzahl, Spaltenanzahl
und Invertierbarkeit von
 ,
, 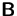 ,
, 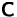 und
und 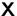 gibt,
so daß die Rechenoperationen in der
Gleichung definiert sind und die Gleichung nach
gibt,
so daß die Rechenoperationen in der
Gleichung definiert sind und die Gleichung nach 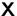 lösbar ist.
lösbar ist.
- (b)
- Bestimmen Sie die Lösung der Gleichung nach
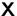 .
.
(Lösung)
- 1.
- Bestimmen Sie den/die stationären Punkt(e) von
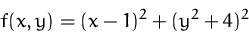
- 2.
- Stellen Sie mit Hilfe der Hessematrix fest, ob es sich um
Minima, Maxima oder Sattelpunkte handelt.
- 3.
- Stellen Sie fest, ob eventuelle Optima global sind.
(Lösung)
Bestimmen Sie 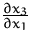 aus der impliziten
Funktion
aus der impliziten
Funktion
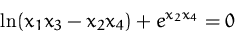
(Lösung)
Berechnen Sie 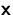 aus
aus 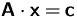 mit
mit
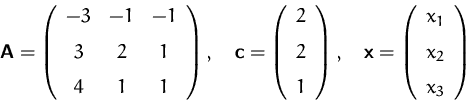
(Lösung)
Bestimmen Sie die maximale Anzahl linear unabhängiger Vektoren in der Vektorenmenge
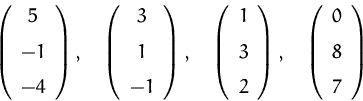
(Lösung)
Bestimmen Sie die stationären Punkte der Funktion
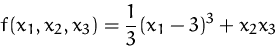
unter den Nebendingungen

mit Langrangemultiplikatoren.
(Lösung)
Lösen Sie das lineare Optimierungsproblem
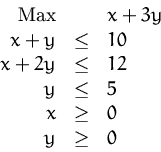
graphisch. Geben Sie die Koordinaten des optimalen Punkts und den
Wert der Zielfunktion im Optimum an.
(Lösung)
Lösen Sie das Optimierungsproblem aus dem vorangegangenen Beispiel
mit Hilfe des Simplexalgorithmus.
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
![]()
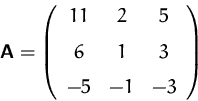
![]()
![]()
![]()
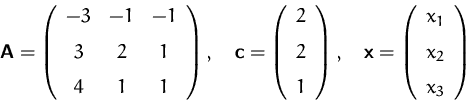
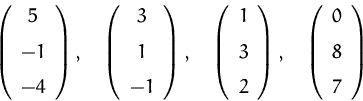
![]()
![]()
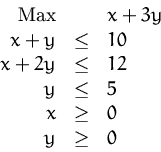
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)