previous: Die Exponentialfunktion up: Elementare Funktionen next: Winkelfunktionen

Die Logarithmusfunktion  

(Graph)

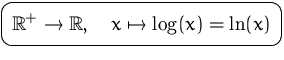
Inverse Funktion zur Exponentialfunktion.

$\mbox{\ovalbox{$\displaystyle {\mathbb R}^+\to{\mathbb R},\quad x\mapsto\log(x)=\ln(x)$}}$

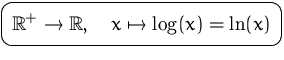
Allgemein: Logarithmus zur Basis $a$

$\mbox{\ovalbox{$\displaystyle {\mathbb R}^+\to{\mathbb R},\quad x\mapsto\log_a(x)$}}$

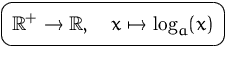
Einschub:

Rechnen mit Exponenten und Logarithmus.

Eine Zahl $y$ heißt Logarithmus zur Basis $a$ der Zahl $x$, falls $a^y=x$. Der Logarithmus ist der Exponent einer Zahl bezüglich einer Basis $a$.Wir schreiben dafür

$$y=\log_a(x)$$

Die wichtigste Basis für den Logarithmus ist die  Eulersche Zahl $e=2,7182818\ldots$ ($\Rightarrow$  natürlicher Logarithmus). Wir schreiben dafür $\ln(x)$ oder $\log(x)$ statt $\log_e(x)$. Wichtig ist auch die Basis 10 ($\Rightarrow$  dekadischer Logarithmus).

UMRECHNUNGSFORMEL:

$\mbox{\ovalbox{$\begin{Beqnarray*} a^x &=& e^{x\,\ln(a)}\\ [1ex] \log_a(x) &=& \frac{\ln(x)}{\ln(a)} \end{Beqnarray*}$}}$

ACHTUNG:

In englischen wirtschaftsmathematischen Büchern steht $\log(x)$ für den dekadischen Logarithmus!

Rechenregeln für Exponenten und Logarithmus:

$$a^{x+y} = a^x\cdot a^y a^{\log_a(x)} = x$$

$$\log_a(x\cdot y) = \log_a(x)+\log_a(y) \log_a(a^x) = x$$

$$\log_a(\frac{x}{y}) = \log_a(x)-\log_a(y) \log_a(1)=0$$

$$\log_a(x^\alpha) = \alpha\cdot\log_a(x) \log_a(a)=1$$

ACHTUNG:

$\log_a(x)$ ist nur für $x\gt$ definiert!
$\log_a(x+y)$ ist nicht gleich $\log_a(x)+\log_a(y)$.