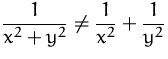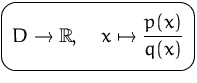
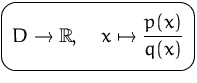
wobei ![]() und
und ![]() Polynome sind und
Polynome sind und
![]() .
.
Einschub:
Rechenregeln für Brüche und Bruchterme.
Seien ![]()
| Regel | Bezeichnung |
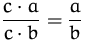 |
Kürzen |
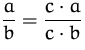 |
Erweitern |
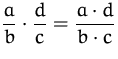 |
Multiplizieren |
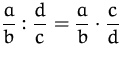 |
Dividieren |
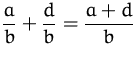 |
|
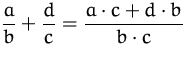 |
Addieren |
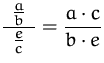 |
Doppelbruch Auflösen |
(Bei der Addition zuerst auf gemeinsamen Nenner bringen!)
BEISPIEL RICHTIG
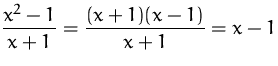
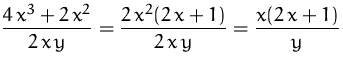
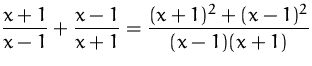
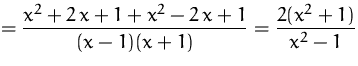
ACHTUNG!
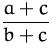 |
ist nicht gleich | |
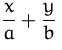 |
ist nicht gleich | 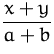 |
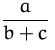 |
ist nicht gleich | 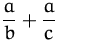 |
BEISPIEL FALSCH
 .
.