

previous: 25. Jänner 1996
next: 5. Oktober 1995
- 1.
- Invertieren Sie die Matrix
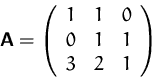
- 2.
- Überprüfen Sie durch die Multiplikation von
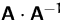 oder
oder 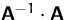 , ob die Inverse richtig berechnet wurde.
, ob die Inverse richtig berechnet wurde.
(Lösung)
- 1.
- Berechnen Sie die Determinante der Matrix

- 2.
- Es sei
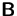 eine
eine 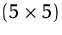 -Matrix mit
-Matrix mit 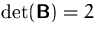 .
.
Berechnen Sie die 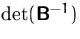 und die
und die 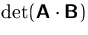 .
.
(Lösung)
- 1.
- Bestimmen Sie die stationären Punkte der Funktion
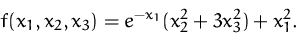
- 2.
- Stellen Sie mit Hilfe der Hessematrix fest, ob es sich bei den
stationären Punkten um Minima, Maxima oder Sattelpunkte handelt.
(Lösung)
Bestimmen Sie die Lösung(en) der Gleichungssysteme
- 1.
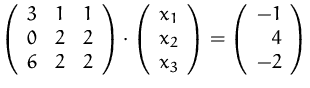
- 2.
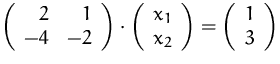
(Lösung)
- (a)
- Bestimmen Sie die Elastizität von
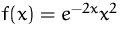
- (b)
- Wo ist
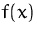 elastisch, unelastisch bzw.
1-elastisch ?
elastisch, unelastisch bzw.
1-elastisch ?
(Lösung)
![\begin{displaymath}
\begin{array}
{rcl}
\max\quad z=x_1+x_2&&\\ [1ex]
\mbox{NB...
... 2x_1-x_2&\le& 3\\ x_2&\le& 1\\ x_1, x_2 &\ge& 0
\end{array}\end{displaymath}](img204.gif)
- (a)
- Lösen Sie das lieare Optimierungsproblem mit dem Simplexalgorithmus.
- (b)
- Lösen Sie das Problem graphisch. (Minimum und Maximum sollen
eingezeichnet werden)
- (c)
- Wie ändert sich die Lösung, wenn die Zusatzbedingung
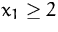 eingeführt wird. (Minimum und Maximum sollen eingezeichnet werden.)
eingeführt wird. (Minimum und Maximum sollen eingezeichnet werden.)
(Lösung)
- (a)
- Bestimmen Sie die Lagrangefunktion für
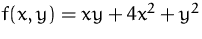 unter der Nebenbedingung:
unter der Nebenbedingung: 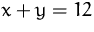 und berechnen Sie alle
stationären Punkte.
und berechnen Sie alle
stationären Punkte.
- (b)
- Stellen Sie fest, ob es sich bei den stationären Punkten um
lokale Maxima, Minima oder Sattelpunkte handelt.
(Lösung)
- (a)
- Berechnen Sie
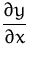 in der impliziten Funktion
in der impliziten Funktion
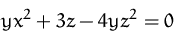
(x, y, z sind die Variablen)
- (b)
- Überprüfen Sie das Ergebnis durch Umformung auf die explizite
Funktion
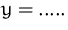 und Bildung der partiellen Ableitung
und Bildung der partiellen Ableitung 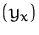 .
.
(Lösung)


© 2. Februar 1999, Josef Leydold
Abteilung für angewandte Statistik und Datenverarbeitung
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)
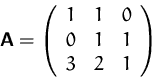
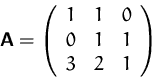

![]()
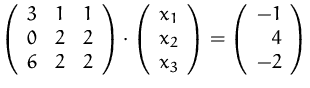
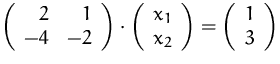
![\begin{displaymath}
\begin{array}
{rcl}
\max\quad z=x_1+x_2&&\\ [1ex]
\mbox{NB...
... 2x_1-x_2&\le& 3\\ x_2&\le& 1\\ x_1, x_2 &\ge& 0
\end{array}\end{displaymath}](img204.gif)
![]()
![[Miran, `Im Bergwerk I']](http://statistik.wu-wien.ac.at/picts/miran/bergwerk1.gif)