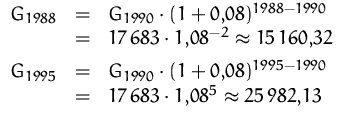Wie groß ist das Guthaben nach 1, 2,
Ein Betrag von ![]() Geldeinheiten wird zu einem Zinssatz von
Geldeinheiten wird zu einem Zinssatz von ![]() (%) angelegt.
(%) angelegt.
Wie groß ist das Guthaben nach 1, 2, ![]() ,
, ![]() Jahren?
Jahren?
LöSUNG:
Guthaben nach einem Jahr:
![]()
Guthaben nach dem zweiten Jahr:
![]()
Guthaben nach dem ![]() -ten Jahr:
-ten Jahr:
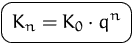
Die Guthaben in den einzelnen Jahren bilden somit eine
geometrische Folge.
Die Formel ![]() läßt sich auf den allgemeinen Fall des
Wertzuwachses bzw. der Wertabnahme eines Kapitals im Zeitablauf
erweitern.
läßt sich auf den allgemeinen Fall des
Wertzuwachses bzw. der Wertabnahme eines Kapitals im Zeitablauf
erweitern.
Es seien ![]() und
und ![]() unterschiedliche Zeitpunkte. Dann ist
unterschiedliche Zeitpunkte. Dann ist

Wenn ![]() , sprechen wir von einer Abzinsung oder
Diskontierung von
, sprechen wir von einer Abzinsung oder
Diskontierung von ![]() auf
auf ![]() .
.
Wenn ![]() wird
wird ![]() auf
auf ![]() aufgezinst.
aufgezinst.
BEISPIEL
Ein Guthaben ![]() auf einem Sparbuch beträgt 1990 17683
Geldeinheiten. Wie hoch war das Guthaben im Jahre 1988 bzw. wie
hoch wird es im Jahr 1995 bei einer Verzinsung von 8% sein?
auf einem Sparbuch beträgt 1990 17683
Geldeinheiten. Wie hoch war das Guthaben im Jahre 1988 bzw. wie
hoch wird es im Jahr 1995 bei einer Verzinsung von 8% sein?