previous: Konvexe und konkave Funktionen up: Krümmung next: Optimierung

Die Hesse-Matrix  

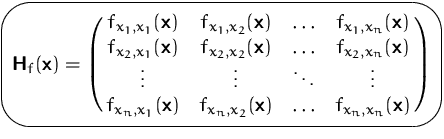
Mit Hilfe der Hesse-Matrix können wir die Krümmung von differenzierbaren Funktionen bestimmen (vgl.).

 

DEFINITION (HESSE-MATRIX)
Die Matrix (vgl.)

$\mbox{\ovalbox{$\displaystyle \mathsfbf{H}_f(\mathsfbf{x}) = \pmatrix{ f_{x_1,... ...fbf{x}) & f_{x_n,x_2}(\mathsfbf{x}) & \ldots & f_{x_n,x_n}(\mathsfbf{x}) } $}}$

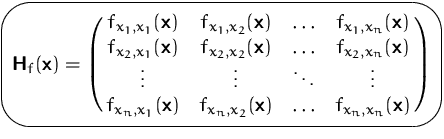
heißt die  Hesse-Matrix von $f$ an der Stelle $\mathsfbf{x}$.

Eine Funktion $f(\mathsfbf{x})$ ist genau dann konvex in $D$, wenn $D\subset{\mathbb R}^n$ konvex ist und die die Hesse-Matrix positiv semidefinit ist für alle $\mathsfbf{x}\in D$.

Die Funktion ist genau dann konkav in $D$, wenn $D\subset{\mathbb R}^n$ konvex ist und die Hesse-Matrix negativ semidefinit ist für alle $\mathsfbf{x}\in D$.

Vorgangsweise:

(1)

Ist $D$ konvex?

(2)

Berechne die Hesse-Matrix $\mathsfbf{H}_f(\mathsfbf{x})$.

(3)

Berechne die allgemeinen Hauptminoren $\vert\tilde\mathsfbf{H}_k\vert$ von  $\mathsfbf{H}_f(\mathsfbf{x})$.

(4)

• Alle Hauptminoren $\vert\tilde\mathsfbf{H}_k\vert \geq 0$ für alle $\mathsfbf{x}\in D$ $\quad\Rightarrow\quad f$ ist konvex.

• Alle geraden Hauptminoren $\vert\tilde\mathsfbf{H}_2\vert,\,\vert\tilde\mathsfbf{H}_4\vert,\,\ldots \geq 0$, alle ungeraden Hauptminoren $\vert\tilde\mathsfbf{H}_1\vert,\,\vert\tilde\mathsfbf{H}_3\vert,\,\ldots \leq 0$ für alle $\mathsfbf{x}\in D$ $\quad\Rightarrow\quad f$ ist konkav.

• Andernfalls ist $f$ in $D$ weder konvex noch konkav.

Jede positiv definite Matrix ist auch positiv semidefinit. In diesem Fall kann die Definitheit auch mit Hilfe der Hauptminoren $\vert\mathsfbf{H}_k\vert$ gezeigt werden (Vorgangsweise).

BEISPIEL
Ist die Funktion konkav oder konvex?

$$f(x,y) = x^4 + x^2 -2\,x\,y + y^2 \quad\mbox{ in }D={\mathbb R}^2$$

(1) Der ${\mathbb R}^2$ ist konvex.

(2) Die Hesse-Matrix lautet

$$\begin{array} {ll} f_x(\mathsfbf{x}) = 4 x^3 + 2\,x -2\,y\q... ...yx}(\mathsfbf{x}) = -2 & f_{yy}(\mathsfbf{x}) = 2 \end{array}$$

$$\mathsfbf{H}_f(\mathsfbf{x}) = \pmatrix{12\,x^2 + 2 & -2 \cr -2 & 2 }$$

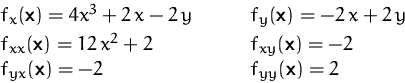
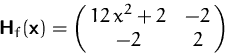
(3) Die allgemeinen Hauptminoren der Hesse-Matrix sind

$\vert\tilde\mathsfbf{H}_1\vert = 12\,x^2 + 2 \geq 0\quad$ bzw. $\quad =2\geq 0$
$\vert\tilde\mathsfbf{H}_2\vert = \det(\mathsfbf{H}_f(\mathsfbf{x})) = 24\,x^2 \geq 0$

(4) Alle Hauptminoren $\geq 0$ für alle $\mathsfbf{x}\in D$

$\quad\Rightarrow\quad f$ ist konvex in $D$.