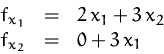previous: Was sind Funktionen in up: Funktionen in mehreren Variablen next: Der Gradient

Partielle Ableitungen  

Wie kann man eine Funktion $f$ in mehreren Variablen differenzieren?

Wir fassen alle Variablen der Funktion -- außer $x_i$ -- als Konstante auf und differenzieren nach $x_i$ nach den bereits bekannten Regeln für das Differenzieren von Funktionen in einer Variable.

Diese Ableitungen heißen die (ersten)  partiellen Ableitungen von $f$ an der Stelle $\mathsfbf{x}$.Schreibweisen:

$\mbox{\ovalbox{$\displaystyle f_{x_i}(\mathsfbf{x})=\frac{\partial f}{\partial x_i}(\mathsfbf{x})$}}$

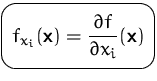
(Die ,,Schreibweisen`` $f'(x)$ und $f'(y)$ für die ersten partiellen Ableitungen nach $x$ bzw. $y$ sindfalsch!)

BEISPIEL
Gesucht sind die ersten partiellen Ableitungen von

$$f(x_1,x_2)=\sin(2\,x_1)\cdot\cos(x_2)$$

$$\begin{array} {rcl} f_{x_1} &=& 2\cdot\cos(2\,x_1) \cdot ... ...mbox{als Konstante betrachtet}} \cdot(-\sin(x_2)) \end{array}$$

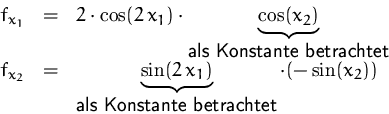
BEISPIEL
Die ersten partiellen Ableitungen von

$$f(x_1,x_2)=x_1^2+3\,x_1\,x_2$$

sind

$$\begin{array} {rcl} f_{x_1}&=&2\,x_1+3\,x_2\\ f_{x_2}&=&0 + 3\,x_1 \end{array}$$